Der Neuling im Digitalaufbau wird sich wundern, dass für die Adern der Fahrstromzuführung hohe Kabelquerschnitte angegeben sind. An diese Vorgaben sollte man sich unbedingt halten! Leider wurde bei keinem Produzenten dafür ein Grund genannt. Bedenken sollte man, wenn man eine Anlage mit zu kleinem Querschnitt aufbaut und es funktioniert nichts, dann schlägt die Freude in Frust um und man zweifelt am Digitalsystem. Da aber dafür ein beträchtlicher finanzieller Betrag ausgegeben wurde, wird man diesen selten in den Sand setzen. Man reist die Verdrahtung wieder raus und baut alles mit größeren Querschnitten neu. Zusätzliche Arbeitszeit und Kosten sind also vorprogrammiert. Deshalb hier einige Argumente für diese Dimensionierung.
Punkt A Die Theorie
Erstens
Fakt ist, die Möglichkeiten einer Digitalsteuerung gegenüber der Analogen sind um ein Vielfaches größer. Deshalb wird es auch vorkommen, dass sich in einem Abschnitt mehrere Loks bewegen. Beispiel: Eine alte H0 Roco – Lok zieht beim Anfahren schon mal 1,2A. Hat man eine Mehrfachtraktion von 3 Loks oder einen Loktyp mit 2 Motoren so sind schnell 3,5A zusammen. Der „Puppenstubendraht“ ist aber nur für eine Dauerlast von 2,0A ausgelegt. Er würde sich erhitzen und die Isolierung weg schmelzen. Dabei kommt es dann unter der Anlage bei kreuzenden Adern zu Kurzschlüssen!
Zweitens
Mit zunehmender Kabellänge nimmt der innere Widerstand zu. Um das auszugleichen, vergrößert man den Kabelquerschnitt. Macht man das nicht, kommt es zu einem Spannungsfall. Hier deshalb etwas Mathe und Physik dazu: Den Widerstand eines Materials kann man bezüglich den geometrischen Abmessungen des Materials darstellen:
R – Widerstand
A – Querschnitt
l – Länge
rho – spezifischer Widerstand
Spezifischer Widerstand ρ (rho) Jedes Material hat einen eigenen Widerstand, der von der Atomdichte und Anzahl der freien Elektronen abhängig ist. Der Widerstand wird deshalb spezifischer Widerstand genannt. Je kürzer die Leitungslänge und je größer der Leitungsquerschnitt des Materials, desto geringer der ohmsche/elektrische Widerstand. Die Abhängigkeit von der Leitungslänge wird dadurch erklärt, dass die Elektronenbewegung auf einer größeren Strecke stärker gehemmt wird, als auf einer kürzeren Strecke. Durch eine Änderung der Leitungslänge und des Querschnitts ändert sich nur der ohmsche Widerstand. Der spezifische Widerstand ist eine Materialkonstante und ist somit ein fest definierter Wert. Der spezifische Widerstand wird auf der Basis von 1 m Länge, 1 mm² Querschnitt bei einer Temperatur von 20°C angegeben.
Formel zur Berechnung:
Beispiele für den spezifischen Widerstand:
Leitungsquerschnitt
Heißt soviel wie: „q“ ist das Ergebnis in mm² wenn man für “I” Ampere (A) einsetzt und für “l” die Länge der Leitung in Meter (m). Der Wert “Uv” gibt die max. Verlustspannung über dem Leiter an. Die Konstante von 0,018 (gerundet) ist der spezifische Widerstand von Kupfer, sollte das verwendete Kabel also kein Kupferkabel sein, dann diesen Wert bitte ersetzten!
Ein Beispiel:
- der spezifische elektrische Widerstand 0,018 Ohm (gerundet für Kupfer)
- der Leitungsquerschnitt 1,5 mm²
- die Gesamtlänge der Leitung 100 m
Der Leitungswiderstand ist klar und wir schließen einfach daraus, dass am Ende einer Leitung nicht das rauskommt, was am Anfang reingeschickt wird. Ein Spannungsverlust ist also gegeben. Dieser “Spannungsfall” kann je nach Länge der Leitung und Leitungsquerschnitt so groß sein, dass wir nicht einmal eine kleine Birne zum Glimmen bringen können. Der Spannungsfall Uv in Volt ist abhängig vom Widerstand im Ohm und der Stromstärke in A (Ampere). In eine Formel gebracht, kann berechnet werden, wie groß der Spannungsfall ist.
Beispiel:
12 Volt Verlust bei einer Leitung von 100 Meter Länge und einem Querschnitt von 1.5 mm² bei einer Stromstärke von 10 A. Ist nicht wenig, oder? Wir brauchen also ein Kabel mit stärkerem Querschnitt und besser als probieren ist rechnen. Berechnet wird der Querschnitt der Leitung mit den Werten für die Stromstärke in A (Ampere), dem spezifischen elektrischen Widerstand in Ohm, der Leitungslänge in Metern und dem Spannungsfall Uv in Volt.
Für unser oben benutzen Werte ergibt sich daraus:
Wenn ich mich nicht verrechnet habe, ergibt das einen Leitungsquerschnitt von 18 mm². Diesen gibt es im Handel nicht, der nächste größere, den wir in einem solchem Fall verwenden müssten, ist 25 mm². Ist natürlich etwas übertrieben diese Rechnung, aber mit den geraden Zahlen lässt es sich so schön rechnen.
Punkt B Die Praxis
Drittens
Bei großen Clubanlagen kann es schon mal vorkommen, dass eine Zuleitung mehrere Meter lang ist und der zu versorgende Abschnitt ebenso. Bei solchen „langen“ Abschnitten hat es sich bewährt, möglichst mehrere Einspeisestellen am Gleisprofil anzulöten. Als grobe Formel würde ich sagen vom Einspeisepunkt bis zur fahrenden Lok sollten nur 2 Schienenstöße dazwischen liegen. Dabei ist der Einbau von langem Gleisprofil in Meterstücken sehr zu empfehlen. Ein Schienenverbinder hat besonders bei brüniertem Gleisprofil einen hohen Übergangswiderstand und ist eine zusätzliche Fehlerquelle wenn er sich lockert. Folgende Kabelquerschnitte kann ich empfehlen:
- vom Trafo zur Digitalzentrale oder Booster 1,5mm², besser 2,5mm²
- von Digitalzentrale oder Booster zum Belegtmelder 1,5mm²
- vom Belegtmelder zum Gleis (Ader rot) 0,75mm², besser 1,5mm²
- vom Belegtmelder zum Gleis (Ader blau) 0,75mm²
- SX-Buskabel (geschirmt) 0,25mm²
- Decoderanschluss H0, TT , N Fahrzeuge 0,14mm²
- Decoderanschluss Z Fahrzeuge 0,055mm²
Die nachfolgende Tabelle zeigt Beispiele für den Einsatz von Kabeln für bestimmte Strombelastungen. Diese Tabelle ist nicht an eine DIN oder VDE Norm angelehnt. Es sind meine eigenen Erfahrungswerte, mit denen man auf der ganz sicheren Seite ist!
| Draht | Litze | ||||
|---|---|---|---|---|---|
| Durchmesser in mm | Querschnitt in mm² | Nennstrom (max.) in A | Aderaufbau ( Stück x mm) Durchmesser | Querschnitt in mm² | Nennstrom (max.) in A |
| 0,56 | 0,25 | 1,4 | 7 x 0,10 | 0,055 | 0,25 |
| 0,6 | 0,28 | 1,8 | 18 x 0,10 | 0,14 | 1,5 |
| 0,66 | 0,34 | 2 | 14 x 0,15 | 0,25 | 3 |
| 0,8 | 0,5 | 3 | 16 x 0,15 | 0,28 | 3,2 |
| 1 | 0,75 | 6 | 7 x 0,25 | 0,34 | 4 |
| 1,13 | 1 | 10 | 16 x 0,20 | 0,5 | 6 |
| 1,38 | 1,5 | 16 | 24 x 0,20 | 0,75 | 9 |
| 32 x 0,20 | 1 | 12 |
|||
| 30 x 0,25 | 1,5 | 16 |
|||
| 50 x 0,25 | 2,5 | 20 |
|||
Viertens
Der wenig versierte Modellbahner wird nun nach der ganzen Theorie fragen wie er seine Kabel „berechnen“ kann. Auch wird er über das Wort „Spannungsfall“ stolpern! Die alte Bezeichnung hierfür ist der Spannungsabfall. Jeder Leiter setzt dem Strom einen Widerstand entgegen. Dabei kann es bei ungenügendem Leitungsquerschnitt zur Erwärmung oder zum Verschmoren der Leitung führen. Um stets auf der sicheren Seite zu sein, muss man einen Leitungsquerschnitt wählen, der dem transportierenden Strom entspricht plus eine Sicherheitsreserve, um auch gegen auftretende Kurzschlüsse gewappnet zu sein. Hier die Berechnungsformel für den Spannungsfall und im Anschluss eine einfache Tabelle zum Ablesen der Werte:
RLtg = (2 * l) / (y * )
- RLtg = Leitungswiderstand in Ohm
- 2* l =2x Leitungslänge (Hin und Rückleitung) in Meter
- y = Leitfähigkeit (für Kupfer ist der Wert 56 einzusetzen)
Ua = I * RLtg
- Ua = Spannungsfall in VoltA = Leitungsquerschnitt in mm²
- I = Strombelastung in Ampere
Rechenbeispiel:
- Beleuchtung für 60 Straßenlaternen à 50mA = 3A
- Leitungslänge 8m
- Leiterquerschnitt 0,25 mm²
RLtg =(2 * 8) / (56 * 0,25) = 16 / 14 = 1,14 Ohm
Ua = 3 * 1,14 = 3,42V
Bei einer Betriebsspannung von 12V liegen dann nur noch etwa 8,58V (12V-3,42V) an. Das sind 71,5% der Betriebsspannung. Die Laternen werden nur glimmen und keine Helligkeit verbreiten.
Anmerkung zur Tabelle: Die Spalte „Leitung in Meter“ bezieht sich als einfache Kabelstrecke von der Spannungsquelle zum Verbraucher. Der Rückweg ergibt sich über die oben vorher angeführte Formel für die in Ua errechneten Werte.
| Spannungsfall bei Querschnitt 0,14 mm² |
||||||||||
| Leitung in Meter | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V |
| 2 | 0,5 | 0,255 | 1 | 0,510 | 2 | 1,020 | 3 | 1,530 | 4 | 2,041 |
| 4 | 0,5 | 0,510 | 1 | 1,020 | 2 | 2,041 | 3 | 3,061 | 4 | 4,082 |
| 6 | 0,5 | 0,765 | 1 | 1,530 | 2 | 3,061 | 3 | 4,592 | 4 | 6,122 |
| 8 | 0,5 | 1,020 | 1 | 2,041 | 2 | 4,082 | 3 | 6,122 | 4 | 8,163 |
| 10 | 0,5 | 1,276 | 1 | 2,551 | 2 | 5,102 | 3 | 7,653 | 4 | 10,204 |
| Spannungsfall bei Querschnitt 0,25 mm² |
||||||||||
| Leitung in Meter | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V |
| 2 | 0,5 | 0,143 | 1 | 0,286 | 2 | 0,571 | 3 | 0,857 | 4 | 1,143 |
| 4 | 0,5 | 0,286 | 1 | 0,571 | 2 | 1,143 | 3 | 1,714 | 4 | 2,286 |
| 6 | 0,5 | 0,429 | 1 | 0,857 | 2 | 1,714 | 3 | 2,571 | 4 | 3,429 |
| 8 | 0,5 | 0,571 | 1 | 1,143 | 2 | 2,286 | 3 | 3,429 | 4 | 4,571 |
| 10 | 0,5 | 0,714 | 1 | 1,429 | 2 | 2,857 | 3 | 4,286 | 4 | 5,714 |
| Spannungsfall bei Querschnitt 0,34 mm² |
||||||||||
| Leitung in Meter | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V |
| 2 | 0,5 | 0,105 | 1 | 0,210 | 2 | 0,420 | 3 | 0,630 | 4 | 0,840 |
| 4 | 0,5 | 0,210 | 1 | 0,420 | 2 | 0,840 | 3 | 1,261 | 4 | 1,681 |
| 6 | 0,5 | 0,315 | 1 | 0,630 | 2 | 1,261 | 3 | 1,891 | 4 | 2,521 |
| 8 | 0,5 | 0,420 | 1 | 0,840 | 2 | 1,681 | 3 | 2,521 | 4 | 3,361 |
| 10 | 0,5 | 0,525 | 1 | 1,050 | 2 | 2,101 | 3 | 3,151 | 4 | 4,202 |
| Spannungsfall bei Querschnitt 0,5 mm² |
||||||||||
| Leitung in Meter | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V |
| 2 | 0,5 | 0,0714 | 1 | 0,143 | 2 | 0,286 | 3 | 0,429 | 4 | 0,571 |
| 4 | 0,5 | 0,143 | 1 | 0,286 | 2 | 0,571 | 3 | 0,857 | 4 | 1,143 |
| 6 | 0,5 | 0,214 | 1 | 0,4286 | 2 | 0,857 | 3 | 1,286 | 4 | 1,713 |
| 8 | 0,5 | 0,286 | 1 | 0,571 | 2 | 1,143 | 3 | 1,714 | 4 | 2,286 |
| 10 | 0,5 | 0,357 | 1 | 0,714 | 2 | 1,429 | 3 | 2,143 | 4 | 2,857 |
| Spannungsfall bei Querschnitt 0,75 mm² |
||||||||||
| Leitung in Meter | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V |
| 2 | 0,5 | 0,048 | 1 | 0,0952 | 2 | 0,190 | 3 | 0,286 | 4 | 0,381 |
| 4 | 0,5 | 0,095 | 1 | 0,190 | 2 | 0,381 | 3 | 0,571 | 4 | 0,762 |
| 6 | 0,5 | 0,143 | 1 | 0,286 | 2 | 0,571 | 3 | 0,857 | 4 | 1,143 |
| 8 | 0,5 | 0,190 | 1 | 0,3811 | 2 | 0,762 | 3 | 1,143 | 4 | 1,524 |
| 10 | 0,5 | 0,238 | 1 | 0,476 | 2 | 0,952 | 3 | 1,429 | 4 | 1,905 |
| Spannungsfall bei Querschnitt 1,5 mm² |
||||||||||
| Leitung in Meter | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V |
| 2 | 0,5 | 0,024 | 1 | 0,048 | 2 | 0,095 | 3 | 0,143 | 4 | 0,190 |
| 4 | 0,5 | 0,048 | 1 | 0,095 | 2 | 0,190 | 3 | 0,286 | 4 | 0,381 |
| 6 | 0,5 | 0,071 | 1 | 0,143 | 2 | 0,286 | 3 | 0,429 | 4 | 0,571 |
| 8 | 0,5 | 0,095 | 1 | 0,190 | 2 | 0,381 | 3 | 0,571 | 4 | 0,762 |
| 10 | 0,5 | 0,119 | 1 | 0,238 | 2 | 0,476 | 3 | 0,714 | 4 | 0,952 |
| Spannungsfall bei Querschnitt 2,5 mm² |
||||||||||
| Leitung in Meter | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V | Strom in A | Ua in V |
| 2 | 0,5 | 0,014 | 1 | 0,029 | 2 | 0,057 | 3 | 0,086 | 4 | 0,114 |
| 4 | 0,5 | 0,029 | 1 | 0,057 | 2 | 0,114 | 3 | 0,171 | 4 | 0,229 |
| 6 | 0,5 | 0,043 | 1 | 0,086 | 2 | 0,171 | 3 | 0,257 | 4 | 0,343 |
| 8 | 0,5 | 0,057 | 1 | 0,114 | 2 | 0,229 | 3 | 0,343 | 4 | 0,457 |
| 10 | 0,5 | 0,071 | 1 | 0,143 | 2 | 0,286 | 3 | 0,429 | 4 | 0,571 |

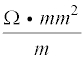
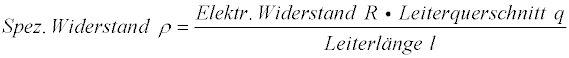
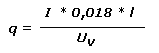
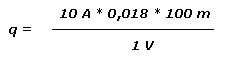
Schreibe einen Kommentar